Mt 13:12

I guess it’s redundant to explicitly state that x and y are elements of the set of natural numbers, but for some reason I hesitate to take it out. So, please don’t let a little redundancy confuse you.

To grasp what this equation is saying, consider a 3-4-5 triangle. 3^2 + 4^2 = 5^2, so from the Pythagorean Theorem, a triangle with sides 3, 4, and 5 must be a right triangle. The Pythagorean Theorem, in general, states that for any right triangle, the sides a, b, and c are related by

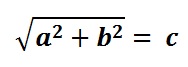
This corresponds to the equation at the top of this post; x = a, y = b, and rho = 2. Unfortunately, c does not also equal y, but that is because rho = 2. If we increased rho to infinity, then b and c would become equal. A few examples show the trend:

As rho gets large, the expression converges on y. Moreover, it doesn’t matter how many elements we sum under the radical. Let’s set y equal to seven and see what happens as we increase rho.

All of these are examples of what mathematicians call an Lp norm. They can be used as a definition of distance in a rho-dimensional space. Some time ago, I was exploring these on my own, and I saw what happens when we take rho to infinity. Though I didn’t know it at the time, I had rediscovered something called the Chebyshev norm.

To intuitively understand what is happening as rho increases, take a look at 3^2 and 4^2. These equal 9 and 16, respectively; a ratio of less than 2:1. Compare that to 6^20 and 7^20. 7^20 is more than twenty times the size of 6^20. Imagine a rectangle that is twenty times taller than it is wide. The diagonal of such a rectangle would be much closer in length to the height than the width. (Strictly speaking, a rectangle’s diameter is not what we are dealing with when rho=20, but twenty dimensions are too many to visualize, and we lack vocabulary. The idea of a diagonal is closely related to the core issue, though.) As rho increases, those diagonals come closer and closer to the longest side of a rho-dimensional block.

As rho goes to infinity, the longest dimension persists. All the lesser lengths drop away. A formal proof of this, and the reason for this post’s title, are left as exercises for the student.